How To Add Fractions - Simple Steps For Anyone

Table of Contents

• What's the Deal with Adding Fractions Anyway?
• How Do You Find a Common Ground When You Add Fractions?
• Making the Parts Match - A Key Step in How to Add Fractions
• Putting It All Together - How to Add Fractions, Piece by Piece
• Example One - Adding 2/3 and 3/4
• Example Two - Adding 1/3 and 2/15
• Example Three - Adding 5/6 and 3/4
• A General Look at How to Add Fractions

Figuring out how to add fractions might seem like a bit of a puzzle at first glance, but honestly, it's a skill anyone can pick up with just a little guidance. We are going to go through the whole thing, step by step, making sure each part makes sense. You know, sometimes numbers just need a bit of coaxing to play nice together, and that's exactly what we'll be doing here.

A lot of people feel a bit stuck when they see those numbers with a line in the middle, but there is a straightforward path to getting them to combine. It just takes a specific approach, more or less, to get them ready for joining up. We will look at the basic idea behind it all, so you can feel good about what you are doing.

• Loomis Singer
• Rhea Ripley Hot
• Holly Peers
• Laila Odom
• Hailey Sigmond

Whether you are just starting out with these kinds of numbers or need a quick refresher, this information is set up to help you. We will go over the things you need to think about and show you some real examples, so you can see how it all works out in practice. So, basically, get ready to make friends with adding fractions.

What's the Deal with Adding Fractions Anyway?

When you are trying to add two fractions, you know, like 2/3 and 3/4, the biggest thing to remember is that the pieces need to be the same size before you can put them together. Imagine trying to add apples and oranges; it just doesn't quite work that way. You need to convert them into a common fruit, or in this case, a common type of fractional piece. This common piece is what we call a shared bottom number, or a least common denominator. It's really just the smallest number that both of the original bottom numbers can divide into without any leftovers, you know?

The idea is that if you have a pie cut into three pieces and another pie cut into four pieces, trying to add a piece from the first pie to a piece from the second pie doesn't make a lot of sense directly. You can't just say "one-third plus one-fourth equals two somethings." You have to cut both pies into an equal number of slices first, so all the slices are the same size. Then, you can count them up properly. That shared number for the bottom of the fraction, the denominator, is that common slice size. So, in a way, it's all about finding a common ground for the numbers to stand on.

• Sexy Red Nudes
• One Golden Summer
• Schnell West Coast
• Joey Gaydos Jr
• Lucious Lopez

Once you find that common number, you then need to change each fraction so it shows how many of those new, equally sized pieces you have. It's like saying, "Okay, if my pie was cut into three pieces, and now I'm cutting it into twelve pieces, how many of those smaller twelve-piece slices is my one-third piece worth?" This step is pretty important because it makes sure you are still talking about the same amount of pie, just shown with different numbers. This process, you know, it just makes everything line up for the final step of putting them together.

How Do You Find a Common Ground When You Add Fractions?

The first big step when you are figuring out how to add fractions is to locate that special number, the least common denominator, often called the LCM. This is the smallest number that both of the bottom numbers, the denominators, can fit into evenly. For instance, if you are looking at 2/3 and 3/4, you need a number that both 3 and 4 can divide into without leaving any remainder. You could list out the multiples of each number until you find a match. For 3, you have 3, 6, 9, 12, 15, and so on. For 4, you have 4, 8, 12, 16, and so on. The smallest number that shows up in both lists is 12. So, 12 is your least common denominator, which is pretty useful.

This idea of finding a common number is really about making sure your parts are comparable. If you are trying to combine things, they need to be measured with the same kind of ruler. The LCM acts like that shared ruler for your fractions. It's not always the product of the two denominators, though it sometimes is. It's the *smallest* shared multiple, which means you might end up with smaller numbers to work with, which is always a plus, you know? Sometimes, one denominator might even be the LCM itself, if the other denominator divides into it cleanly. For example, with 1/3 and 2/15, the number 15 is a multiple of 3, so 15 itself becomes the LCM. It just makes things a little simpler, doesn't it?

To find this number, you can, as a matter of fact, list out the multiples of each denominator. You just keep going until you spot the first number that appears in both lists. Another way, if you are familiar with it, is to use prime factorization, but for many common fraction pairs, simply listing multiples is often the quickest way to get to that shared value. Once you have this number, you are well on your way to getting your fractions ready to combine. It's a foundational step, really, for getting them to line up properly, so.

Making the Parts Match - A Key Step in How to Add Fractions

Once you have found that least common denominator, the next thing you need to do when you are learning how to add fractions is to change each of your original fractions into an equivalent one that has this new common bottom number. This means you are essentially resizing the pieces of your whole without changing the actual amount they represent. For example, if you had 2/3 and you found that 12 was your common bottom number, you would ask yourself, "What do I multiply 3 by to get 12?" The answer is 4. So, you must also multiply the top number, the numerator, by that same 4. This makes 2/3 become 8/12. It's like cutting each of those original three slices into four smaller slices, giving you eight pieces out of a total of twelve, you know?

The key here is to always do the same thing to both the top and the bottom of the fraction. Whatever you multiply the bottom number by to get your common denominator, you absolutely must multiply the top number by that very same value. This keeps the fraction honest, so to speak; it keeps its value exactly the same. You are just showing it in a different way, with smaller, more numerous pieces. This step is pretty important because if you only change the bottom number, you are changing the actual amount the fraction stands for, and that would mess up your whole calculation. So, basically, it's about maintaining balance.

Let's say you have 3/4, and your common bottom number is 12. You would figure out that 4 needs to be multiplied by 3 to get 12. So, you also multiply the top number, 3, by 3. This changes 3/4 into 9/12. Now, both of your fractions, 8/12 and 9/12, have the same size pieces, meaning they both have 12 as their bottom number. They are now ready to be put together. This transformation is what makes adding them possible and straightforward, you know, it just lines everything up for you.

Putting It All Together - How to Add Fractions, Piece by Piece

After you have done the work of finding the common bottom number and changing your fractions to match it, the actual adding part of how to add fractions is surprisingly simple. You just add the top numbers, the numerators, together. The bottom number, the common denominator, stays exactly the same. It's like if you have 8/12 and 9/12; you are just counting how many of those twelfth-sized pieces you have in total. So, 8 plus 9 gives you 17. The bottom number remains 12. Your answer becomes 17/12. It's really that straightforward once the initial setup is done, you know?

Think of it this way: if you have eight slices of a pizza that was cut into twelve pieces, and then you get nine more slices from another pizza also cut into twelve pieces, you just count up all your slices. You now have seventeen slices in total, and each slice is still a twelfth of a pizza. You don't add the "twelfths" together to get "twenty-fourths"; the size of the piece doesn't change, only the count of the pieces does. This is a common point where people sometimes get a little confused, but once you get that concept, it's pretty clear, you know?

Sometimes, your final answer might be what we call an "improper fraction," like 17/12, where the top number is bigger than the bottom one. This just means you have more than one whole. You can leave it like that, or you can change it into a mixed number, which is a whole number and a fraction. For 17/12, you can see that 12 goes into 17 one time with 5 left over. So, 17/12 is the same as 1 and 5/12. This step is just about presenting your answer in a different way, if you want to, you know, for clarity or just for a different kind of look at the total amount.

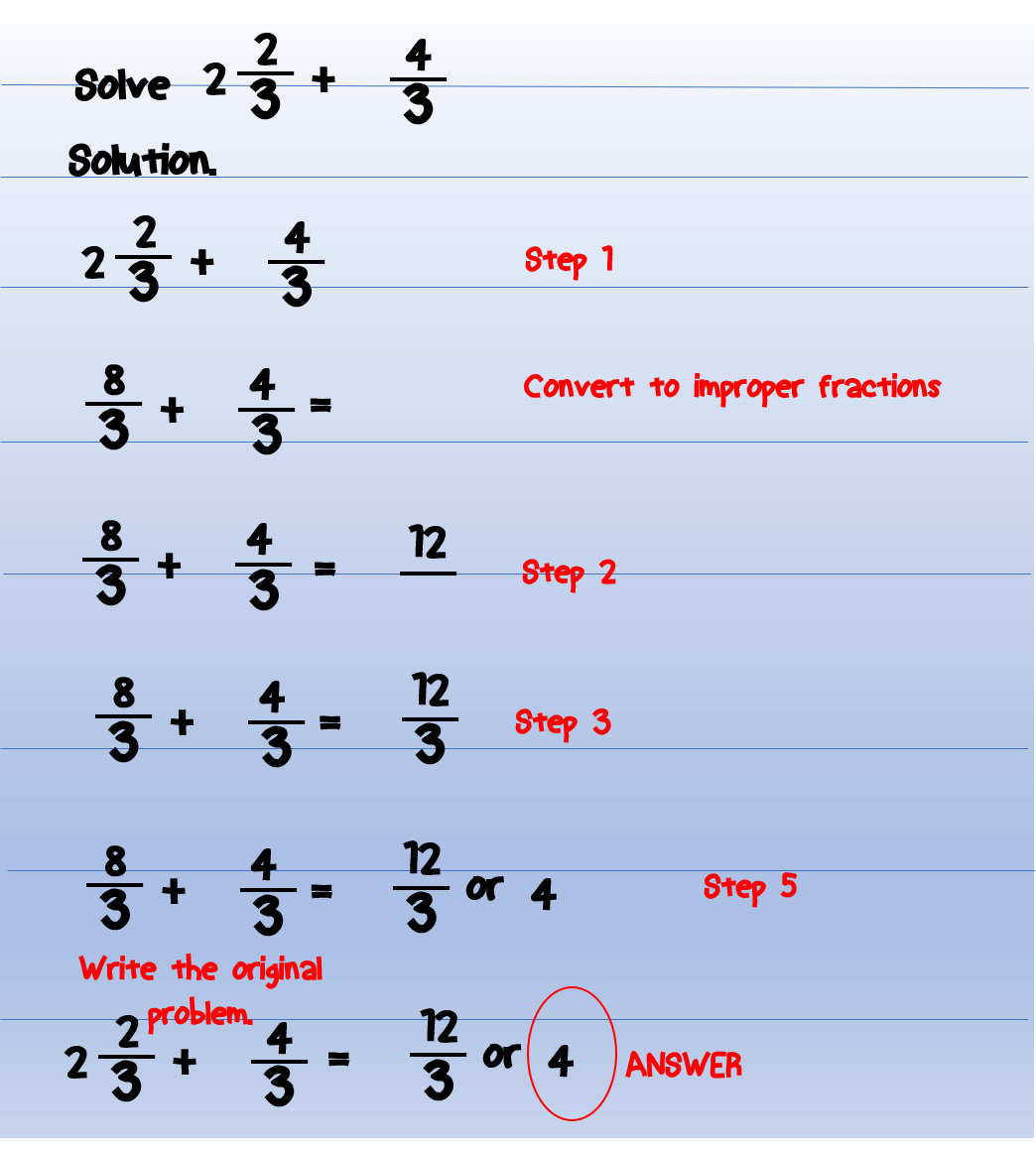
Example One - Adding 2/3 and 3/4

Let's take a look at our first example from "My text": adding 2/3 and 3/4. The very first thing we need to do is find the smallest number that both 3 and 4 can divide into. If we list out the multiples for 3, we get 3, 6, 9, 12, 15, and so on. For 4, we get 4, 8, 12, 16, and so on. The smallest number that shows up in both lists is 12. So, our least common denominator, our shared bottom number, is 12. That's the groundwork, you know, for getting these fractions ready.

Now, we need to change each fraction so it has 12 at the bottom. For 2/3, we ask, "What do we multiply 3 by to get 12?" The answer is 4. So, we multiply both the top (2) and the bottom (3) by 4. This turns 2/3 into 8/12. It's the same amount, just cut into smaller, more numerous pieces. For 3/4, we ask, "What do we multiply 4 by to get 12?" That would be 3. So, we multiply both the top (3) and the bottom (4) by 3. This changes 3/4 into 9/12. Now both fractions are talking about pieces of the same size, which is pretty handy, you know?

With both fractions now having the same bottom number, 8/12 and 9/12, we can simply add their top numbers together. We take 8 and add 9, which gives us 17. The bottom number, 12, stays the same. So, the sum of 2/3 and 3/4 is 17/12. As mentioned earlier, this is an improper fraction, meaning the top number is bigger than the bottom. If you want to, you can convert 17/12 into a mixed number. 12 goes into 17 one time, with 5 left over. So, 17/12 is the same as 1 and 5/12. This shows you, you know, how the whole process unfolds.

Example Two - Adding 1/3 and 2/15

Let's move on to another example from "My text": adding 1/3 and 2/15. The first step is, as always, to find the least common denominator for 3 and 15. If we list the multiples of 3, we have 3, 6, 9, 12, 15, and so on. For 15, the first multiple is 15. Since 15 is already a multiple of 3, the smallest number that both 3 and 15 can divide into evenly is 15 itself. So, our common bottom number is 15. This is a nice situation because one of our fractions already has the common denominator, you know?

Now we adjust our fractions. The fraction 2/15 already has 15 as its bottom number, so we don't need to change it at all. It's already good to go. For 1/3, we need to change it to have 15 at the bottom. We ask, "What do we multiply 3 by to get 15?" The answer is 5. So, we multiply both the top (1) and the bottom (3) by 5. This changes 1/3 into 5/15. Now both fractions, 5/15 and 2/15, are set up with the same size pieces, which is pretty convenient, really.

With both fractions sharing the same bottom number, 5/15 and 2/15, we can simply add their top numbers together. We take 5 and add 2, which gives us 7. The bottom number, 15, stays the same. So, the result of adding 1/3 and 2/15 is 7/15. This fraction is not improper, as the top number is smaller than the bottom, so it's already in a pretty standard form. This particular example shows that sometimes the common denominator is one of the original denominators, which can make things a little quicker, you know?

Example Three - Adding 5/6 and 3/4

Our next example from "My text" involves adding 5/6 and 3/4. Just like before, the very first thing we must do is find the least common denominator for 6 and 4. Let's list the multiples. For 6, we have 6, 12, 18, 24, and so on. For 4, we have 4, 8, 12, 16, and so on. The smallest number that appears in both lists is 12. So, 12 is our common bottom number for these two fractions. This number is what helps us make the pieces comparable, you know?

Now, we need to change each fraction to have 12 as its bottom number. For 5/6, we ask, "What do we multiply 6 by to get 12?" The answer is 2. So, we multiply both the top (5) and the bottom (6) by 2. This changes 5/6 into 10/12. This step is about making sure the amount represented by the fraction stays the same, just with a different way of showing it. For 3/4, we ask, "What do we multiply 4 by to get 12?" That would be 3. So, we multiply both the top (3) and the bottom (4) by 3. This changes 3/4 into 9/12. Now both fractions, 10/12 and 9/12, are ready to be combined, which is pretty neat.

With both fractions now sharing the same bottom number, 10/12 and 9/12, we can simply add their top numbers together. We take 10 and add 9, which gives us 19. The bottom number, 12, stays the same. So, the sum of 5/6 and 3/4 is 19/12. This is another example of an improper fraction, where the top number is larger than the bottom. You can, if you wish, change 19/12 into a mixed number. 12 goes into 19 one time, with 7 left over. So, 19/12 is the same as 1 and 7/12. This example, you know, really shows the general process at work.

A General Look at How to Add Fractions

When you are trying to add fractions, the main idea, as we have seen, is to make sure the pieces you are adding are all the same size. This means getting a shared bottom number, which is often called the least common denominator. You find this number by looking for the smallest multiple that both of the original bottom numbers can divide into without any bits left over. It's a bit like finding a common measurement unit for different items, so they can be accurately counted together, you know?

Once you have that shared bottom number, you adjust each fraction. You figure out what you multiplied the original bottom number by to get the new common one, and then you do the exact same multiplication to the top number. This step is super important because it makes sure you are not changing the value of the fraction, just how it looks. It's still the same amount, just broken into smaller, equal parts that match the new common size. This keeps everything fair and square, basically, for the next step.

Finally, with all your fractions now showing the same size pieces at the bottom, you just add the top numbers together. The bottom number stays put; it's just telling you the size of the pieces, not how many there are. So, you simply count up the total number of those equally sized pieces. Sometimes your answer might have a bigger number on top than on the bottom, which is perfectly fine, or you can change it into a whole number with a fraction part if you like. This whole process, you know, it just helps you combine different fractional amounts into a single, clear total.

This article has gone over how to add fractions by finding a common denominator, changing fractions to match it, and then putting the top numbers together. We looked at examples like 2/3 and 3/4, 1/3 and 2/15, and 5/6 and 3/4 to show the steps in action.