There's something quite interesting about how we measure things, even in the most abstract sense. It's like giving a "norm cheers" to different qualities or behaviors, acknowledging their unique ways of being evaluated. Sometimes, what we measure isn't a simple length or a straightforward gap between two points. It might be something else entirely, a property that shows up when things combine or multiply. That, is that, a pretty different way to look at how we assess value.
You see, it's not always about how far apart two things are. In some respects, it's about how they behave together, what kind of outcome their interaction produces. It's a bit like cheering for a team not just because they ran the fastest, but because of how well they passed the ball or how their individual efforts added up to a collective success. There are, apparently, many ways to give a "norm cheers" to something, depending on what aspect you want to highlight.
This idea of different measurements, and what they truly represent, can get a little complex. It brings up questions about why certain measures exist, what they actually tell us, and where we can go to learn more about them. It's really about trying to grasp these varied ways of evaluating, so we can give the right kind of "norm cheers" in any given situation.
Table of Contents
- What Exactly Are We Measuring with These "Norm Cheers"?
- Finding Your Way to Learn About "Norm Cheers"
- Are All "Norm Cheers" Created Equal?
- The Absolute Value - A Simple "Norm Cheers"
- How Do We Give "Norm Cheers" to Operators?
- The "Norm Cheers" of a Matrix - A Deeper Look
- When a "Norm Cheers" Isn't About Distance
- The Fundamental Idea Behind "Norm Cheers"
What Exactly Are We Measuring with These "Norm Cheers"?
When we talk about certain kinds of algebraic measures, it becomes pretty clear that they aren't always about how far apart things are. This is, you know, a different sort of evaluation. Instead, these particular ways of giving a "norm cheers" are really about how things act when they are multiplied together. It’s a measure of their combined behavior, which is, in a way, quite a fascinating concept to consider.
For instance, some of these evaluations might tell us something about the result of a multiplication, perhaps even showing up as a squared value. It’s not just a straightforward line segment length, but rather a value that emerges from how elements interact in a multiplicative sense. So, it's like a special kind of "norm cheers" that celebrates the product, not just the individual components or their separation.
This means we are looking at something beyond the usual idea of physical space or separation. It’s about a deeper, more abstract property that comes from how numbers or elements combine. It truly gives us a different perspective on what it means to give a "norm cheers" to a mathematical entity, focusing on its operational characteristics.
The very nature of this kind of "norm cheers" suggests that our usual ideas of measurement need to expand. We're not just pulling out a ruler here. We're observing how things grow or shrink, or change, when they are put together in a specific way. It's a way of appreciating the inner workings of an algebraic structure, you know, seeing what makes it tick.
It’s almost like, when you consider it, we are trying to find a single number that summarizes the 'oomph' or the 'impact' of a multiplicative process. This kind of "norm cheers" is less about how much space something takes up and more about how much influence it has in a product. That, is quite a shift in thinking for many people, especially if they are used to only thinking about distance.
Finding Your Way to Learn About "Norm Cheers"
It’s a common situation to find yourself needing to grasp ideas like l1 and l2 ways of giving a "norm cheers," even if you don't have a formal background in higher mathematics. Many people, for example, might come across these concepts in fields like data science or engineering, where they become, you know, quite important tools. The desire to really understand how these different evaluations work and what they represent is a very natural one.
When you're looking for good places to learn these things, the search can be a bit of a challenge. You want resources that explain not just the definitions, but also the practical implications of each "norm cheers." It's about finding explanations that help you see the bigger picture, rather than just memorizing formulas. You need to know, essentially, how they function in real situations and what their purpose is.
The quest for appropriate sources is, actually, a very personal one. What works for one person might not work for another. Some prefer visual explanations, others prefer detailed written accounts, and still others learn best by doing examples. The key is to keep looking until you find that material that truly clicks for you, helping you to truly appreciate these "norm cheers."
It's not enough, perhaps, to just see a definition. You want to see how these different "norm cheers" are applied, what problems they help solve, and why they were created in the first place. This deeper level of understanding is what really makes the concepts stick, and helps you feel more confident in your grasp of these mathematical tools. It's a journey of discovery, really, to get to that point.
So, when someone says they are trying to find the right materials to learn about these different ways of giving a "norm cheers," you can certainly relate. It’s about more than just getting the facts; it’s about building a solid foundation of knowledge that makes sense. That, is the goal for anyone trying to wrap their head around these kinds of abstract measures.
Are All "Norm Cheers" Created Equal?
There's a natural curiosity that pops up when you encounter different types of "norm cheers." For example, someone might be quite familiar with lp and l∞ ways of evaluating things, but then wonder about c0 and c1. Are these simply different names for similar concepts, or do they represent entirely distinct approaches to measurement?
This question gets at the heart of how these various "norm cheers" are defined. If you know one set of definitions, you might naturally assume a pattern for others. But sometimes, the way a specific "norm cheers" is set up can be, you know, quite unique, requiring a fresh look at its underlying rules. It's not always a simple extension of what you already know.
Understanding these distinctions is pretty important, as each type of "norm cheers" has its own specific use and meaning. It's like having different tools in a toolbox; while they all help build something, each one is designed for a particular task. So, figuring out if these different "norm cheers" are truly defined in their own unique ways is a key part of truly grasping the subject.
It can be a little confusing, actually, when you have a good handle on some concepts but then encounter others that seem related but are not immediately clear. The question of whether the former are defined in the same vein as the latter is a very reasonable one to ask. It shows a desire to connect the dots and build a coherent picture of how these "norm cheers" fit together.
The Absolute Value - A Simple "Norm Cheers"
When we talk about real numbers, there's a very straightforward way to give a "norm cheers" to a number, and that's simply its absolute value. It's, you know, perhaps the most basic form of this kind of evaluation that many people learn early on. It just tells you how far a number is from zero, without caring about its direction.
This particular "norm cheers" is, in some respects, the simplest example of a measure that satisfies all the necessary properties of a norm. It's easy to understand and apply. For real numbers, it's the one and only way we commonly use to measure their "size" in this specific sense. It's pretty fundamental, really, to how we think about the magnitude of numbers.
So, when you consider the vastness of mathematical concepts, it’s a bit comforting to have such a clear and singular example. The absolute value is a foundational "norm cheers" that helps us build up to more complex ideas. It's the starting point for understanding how these types of measures work, and how they provide a consistent way to evaluate things.
How Do We Give "Norm Cheers" to Operators?
Moving on from simple numbers, we also have ways to give a "norm cheers" to operators or matrices. This is where things can get a bit more involved. An operator norm, for instance, is a specific type of evaluation that's linked to how we measure vectors. It's like, you know, a way to assess the "strength" or "impact" of a transformation.
This kind of "norm cheers" for an operator is defined by looking at how much it can stretch or scale vectors. It's basically the maximum amount of stretching that the operator can do to any non-zero vector, after you account for the vector's own size. What's interesting is that this "norm cheers" changes depending on which vector measure you start with.
So, if you use one way to measure vectors, you'll get one kind of operator "norm cheers." If you use another, you'll get a different one. For example, when you use the familiar Euclidean measure for vectors, which is like finding the straight-line length, the operator "norm cheers" takes on a specific form. It's a pretty flexible concept, in that way.
It's not just a single, fixed value for every operator. Instead, it adapts to the context of the vector measure you're using. This makes the operator "norm cheers" a powerful tool for understanding how transformations behave, giving us a way to quantify their effect on different kinds of vector spaces. It’s really quite a clever system, if you think about it.
This particular "norm cheers" gives us a way to compare different operators and understand their properties. It tells us how much an operator can amplify or diminish the size of vectors. It's a critical concept for anyone working with linear transformations, as it provides a consistent method for evaluating their behavior. It’s, basically, a way to put a number on how "powerful" an operator is.
The "Norm Cheers" of a Matrix - A Deeper Look
When we get to matrices, the idea of a "norm cheers" can become even more intricate. Someone might learn that a matrix's norm involves the square root of the largest eigenvalue, multiplied by the matrix's transpose and then the matrix itself. This is, you know, a very specific and somewhat complex way to arrive at an evaluation.
It's the kind of definition that can make you pause and wonder about the underlying logic. You might find yourself asking for more explanation, wanting to understand why this particular combination of operations gives us a meaningful "norm cheers" for a matrix. It’s not immediately intuitive for everyone, and that's perfectly fine.
The request for further explanation is, actually, a sign of a curious mind wanting to go beyond just the formula. It's about wanting to grasp the intuition behind why this specific calculation provides a useful measure of a matrix's overall "size" or "influence." This kind of "norm cheers" is quite important in many areas, from data analysis to physics, so understanding its roots is key.
So, when someone asks for a deeper dive into this particular "norm cheers" for a matrix, they are looking for more than just the steps. They want to understand the 'why' behind it, the reasoning that connects these seemingly disparate mathematical concepts into a single, coherent measure. That, is a very good question to ask, really.
When a "Norm Cheers" Isn't About Distance
It’s an important point to remember that just because something is called a "norm cheers," it doesn't always mean it's strictly measuring distance. We touched on this earlier, but it's worth reiterating. If a "norm cheers" isn't a direct measure of how far apart things are, then you can't simply say that an equality involving it directly implies a spatial relationship. This is, you know, a crucial distinction.
The idea that a "norm cheers" can represent something other than distance might be a bit counter-intuitive at first, especially if your initial exposure to the concept was through geometric examples. But in abstract mathematics, these evaluations can capture a wide range of properties, not just physical separation. So, when you see an equation, you can't just assume it's talking about how far something is from something else.
This means we need to be careful about the conclusions we draw. If a "norm cheers" is, say, about multiplicative behavior, then an equality using that norm tells us something about that behavior, not necessarily about how close two points are in space. It's a subtle but very important difference in how we interpret these mathematical statements.
It's pretty much about recognizing the specific nature of each "norm cheers." Each one serves a particular purpose, and its meaning is tied to its definition. So, if a "norm cheers" is designed to capture something other than distance, then its implications will also be different. It's about being precise in our understanding, which is, in some respects, what mathematics is all about.
The Fundamental Idea Behind "Norm Cheers"
At its core, a "norm cheers" is, well, a norm. This might sound like a circular statement, but it actually points to something quite fundamental. It means that once something is established as a norm, it possesses a certain set of properties that make it a consistent and reliable way to evaluate things. It's like saying, "a rule is a rule" – it means it has a defined structure and behavior.
This fundamental nature means that these "norm cheers" satisfy certain conditions, regardless of what specific quantity they are measuring. For instance, an operator "norm cheers" will always behave in predictable ways, even when dealing with orthogonal or arbitrary elements. It's this consistency that makes them so valuable in mathematics and its applications.
So, even if the specific calculation changes, or the property being measured shifts from distance to multiplicative behavior, the underlying principles of what makes something a "norm cheers" remain constant. This provides a solid framework for understanding these various evaluations, giving us a common ground to compare them. It's, you know, quite a unifying concept.
The fact that an operator "norm cheers" holds true for every orthogonal and arbitrary case highlights its robustness. It means it's a very general and widely applicable way to assess operators. This kind of reliability is what makes these abstract measures so useful in building complex mathematical models and theories. It's a testament to their well-defined nature.
Related Resources:
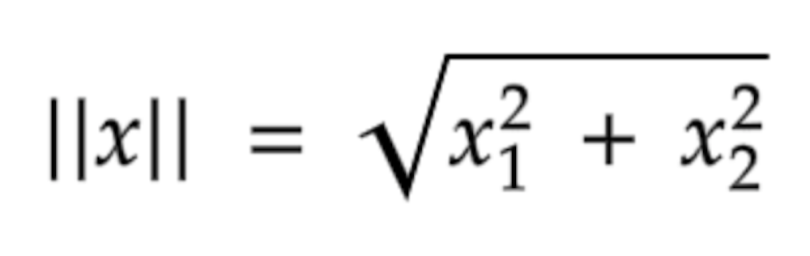
:max_bytes(150000):strip_icc()/folkways-mores-taboos-and-laws-3026267finalversion-5c8fe5a646e0fb000187a359.png)

Detail Author:
- Name : Libbie Morar
- Username : ethyl.lindgren
- Email : shields.royal@gmail.com
- Birthdate : 1971-12-25
- Address : 8701 Alfonzo Roads North Dimitri, MA 41787-4064
- Phone : (215) 539-5089
- Company : Lind-Kunze
- Job : Funeral Attendant
- Bio : Nobis cum veniam et molestias eos. Provident temporibus et tempore. Inventore quo illo quod ut.
Socials
facebook:
- url : https://facebook.com/jedmarvin
- username : jedmarvin
- bio : A et ex inventore rerum. Est suscipit ab voluptatem veniam saepe perferendis.
- followers : 5344
- following : 2010
twitter:
- url : https://twitter.com/jmarvin
- username : jmarvin
- bio : Et iste ullam non iure assumenda voluptas amet. Officia dolor ducimus culpa dolores. Veniam nobis deleniti ex ut et deserunt.
- followers : 4488
- following : 1506
tiktok:
- url : https://tiktok.com/@jed.marvin
- username : jed.marvin
- bio : Dolorem nulla rerum qui est dicta enim. Voluptas qui sunt ea adipisci delectus.
- followers : 4342
- following : 459